Stefan problem

In mathematics and its applications, particularly to phase transitions in matter, a Stefan problem (also Stefan task) is a particular kind of boundary value problem for a partial differential equation (PDE), adapted to the case in which a phase boundary can move with time. The classical Stefan problem aims to describe the temperature distribution in a homogeneous medium undergoing a phase change, for example ice passing to water: this is accomplished by solving the heat equation imposing the initial temperature distribution on the whole medium, and a particular boundary condition, the Stefan condition, on the evolving boundary between its two phases. Note that this evolving boundary is an unknown (hyper-)surface: hence, Stefan problems are examples of free boundary problems.

Contents

Historical note

The problem is named after Jožef Stefan, the Slovene physicist who introduced the general class of such problems around 1890, in relation to problems of ice formation. This question had been considered earlier, in 1831, by Lamé and Clapeyron.

Premises to the mathematical description

From a mathematical point of view, the phases are merely regions in which the coefficients of the underlying PDE are continuous and differentiable up to the order of the PDE. In physical problems such coefficients represent properties of the medium for each phase. The moving boundaries (or interfaces) are infinitesimally thin surfaces that separate adjacent phases; therefore, the coefficients of the underlying PDE and its derivatives may suffer discontinuities across interfaces.

The underlying PDE is not valid at phase change interfaces; therefore, an additional condition—the Stefan condition—is needed to obtain closure. The Stefan condition expresses the local velocity of a moving boundary, as a function of quantities evaluated at both sides of the phase boundary, and is usually derived from a physical constraint. In problems of heat transfer with phase change, for instance, the physical constraint is that of conservation of energy, and the local velocity of the interface depends on the heat flux discontinuity at the interface.

Mathematical formulation

The one-dimensional one-phase Stefan problem

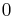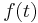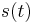Consider an semi-infinite one-dimensional block of ice initially at melting temperature u≡0 for x ∈ [0,+∞[. The ice is heated from the left with heat flux f(t). The flux causes the block to melt down leaving an interval [0,s(t)] occupied by water. The melt depth of the ice block, denoted by s(t), is an unknown function of time; the solution of the Stefan problem consists of finding u and s such that

\begin{align} \frac{\partial u}{\partial t} &= \frac{\partial^2 u}{\partial x^2} &&\text{in } \{(t,x): 0 < x < s(t), t>0\}, && \text{the heat equation},\\ -\frac{\partial u}{\partial x}(0, t) &= f(t), && t>0, &&\text{the Neumann condition at the left end of the ice block describing the given heat flux}, &&\\ u\big(s(t),t\big) &= 0, && t>0, &&\text{the Dirichlet condition at the right end of the block setting the temperature to that of melting/freezing},\\ \frac{\mathrm{d}s}{\mathrm{d}t} &= -\frac{\partial u}{\partial x}\big(s(t), t\big), && t>0, &&\text{Stefan condition},\\ u(x,0) &= 0, && x\geq 0, &&\text{initial temperature distribution},\\ s(0) &= 0, && &&\text{initial melt depth of the ice block}. \end{align}

The Stefan problem also has a rich inverse theory, where one is given the curve s and the problem is to find u or f.

Applications

The solution of the Cahn–Hilliard equation for a binary mixture demonstrated to coincide well with the solution of a Stefan problem.[1]

See also

Notes

  1. ^ F. J. Vermolen, M.G. Gharasoo, P. L. J. Zitha, J. Bruining. (2009). Numerical Solutions of Some Diffuse Interface Problems: The Cahn-Hilliard Equation and the Model of Thomas and Windle. IntJMultCompEng,7(6):523–543.

References

Bibliography

External links